Examen corrigé: analyse des images (partie images 2D)

Cette page présente un examen corrigé du module d’analyse des images de 2D. Pour rappel, l’examen écrit représente 50% de la note finale.

• Durée : 1h00

• Tous documents autorisés. Calculatrices autorisées. Toute communication durant l’examen est interdite.

L’examen est noté sur vingt points. Il est constitué de deux parties: des questions de cours sur douze points et un exercice sur huit points.

Questions (12 points)

Les questions sont indépendantes.

Question 1

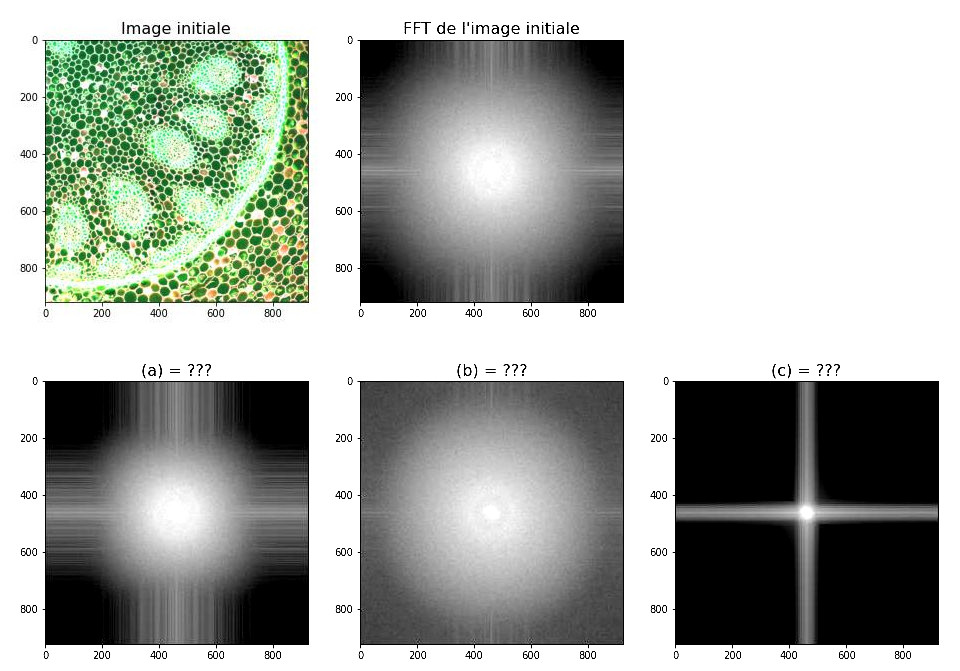
Fig. 1 Images d’une racine de plante, altérée par trois filtres différents. La seconde ligne représente les spectres de Fourier.

(2 points) La seconde ligne de l’image ci-dessus représente les spectres de Fourier correspondant à l’image de la racine de plante filtrée de trois manières différentes. Associer à chaque spectre de Fourier (a), (b) et (c) le filtre correspondant parmi les trois possibilités ci-dessous:

1. un filtre gaussien de variance \(\sigma=1\),

2. un filtre gaussien de variance \(\sigma=10\),

3. un filtre d’augmentation de la netteté (sharpening).

Indication

1. (a) (léger filtre passe-bas)

2. (c) (filtre passe-bas très fort)

3. (b) (le sharpening restaure des hautes fréquences)

Question 2

(2 points) Pour convertir une image couleur encodée en rouge-vert-bleu (RGB) vers une image en niveaux de gris \(Y\), on utilise la formule ci-dessous:

\[Y = 0,2125 R + 0,7154 G + 0,0721 B\]

À quoi correspondent les coefficients de pondération \(0,2125\), \(0,7154\) et \(0,0721\)? Pourquoi ne calcule-t-on pas simplement l’intensité moyenne \(Y = \frac{1}{3}(R + G + B)\)?

Indication

Les coefficients de pondération correspondent aux sensibilités de l’œil humain (proportion de cônes sensibles respectivement au rouge, au vert et au bleu). Si l’on calcule l’intensité moyenne sans pondération, l’image en niveaux de gris ne correspond plus à la luminance perceptuelle.

Question 3

(2 points) Quel est l’intérêt d’utiliser des descripteurs de points d’intérêt qui soient binaires plutôt que des descripteurs en nombres flottants? Donner un exemple d’un tel descripteur binaire.

Indication

Les descripteurs de points d’intérêt sont généralement utilisés pour faire de l’appariement entre images, ce qui nécessite de calculer des distances deux à deux entre toutes les paires de points. L’utilisation de descripteurs binaires permet d’utiliser des distances rapides à calculer, comme la distance de Hamming.

Le descripteur BRIEF fonctionne sur ce principe.

Question 4

Fig. 2 Étiquette d’une bouteille de vin. Le texte « Mis en Bouteille au Château » est déformé.

(2 points) Le texte de l’image de l’image ci-dessus est déformé. Peut-on corriger cette déformation et remettre le texte parfaitement à plat et à l’horizontale avec les méthodes vues en cours? Si oui, laquelle? Si non, pourquoi?

Indication

Non, les méthodes de redressement vues en cours ne permettent de traiter que des déformations projectives (des homographies). Cette déformation est une projection cyclindrique qui ne peut pas s’approcher par une matrice d’homographie.

Il existe d’autres méthodes mais elles n’ont pas été présentées en cours.

Question 5

(2 points) On cherche à appliquer l’algorithme de segmentation par ligne de partage des eaux (watershed) sur une image binaire, c’est-à-dire dont les pixels sont soit noir, soit blanc. Quelle stratégie adopter pour choisir les marqueurs initiaux, c’est-à-dire les sources du watershed?

Indication

Une possibilité courante est de calculer la carte de distance signée puis de sélectionner comme marqueurs initiaux les maxima locaux de cette carte. Cela permet de placer un marqueur au centre de chaque objet.

Question 6

(2 points) Avec vos propres mots, expliquer brièvement pourquoi le filtre de Sobel permet de réaliser une détection de contours.

Indication

Le filtrage de Sobel réalise un calcul de gradient local (dérivée de l’intensité des pixels selon les lignes et les colonnes). Un contour est une région de l’image où l’intensité change brutalement, ce qui implique un gradient élevé. Dans les zones sans contour, l’intensité est homogène et le gradient est faible. C’est pour cette raison que le filtrage de Sobel donne une activation élevée près des contours.

Exercice (8 points)

Fig. 3 Page de texte mal scannée.

Fig. 4 Page de texte redressée.

Fig. 5 Symboles détectées.

Fig. 6 Zoom sur les détections. Le rectangle sombre entoure le symbole de référence.

Dans cet exercice, on imagine un système permettant automatiquement de retrouver un symbole dans une page d’un manuscrit historique. Les images ci-dessus illustrent la suite de traitements sur une leçon mathématique datant de 1788, donnée à André Ampère par le père Daburon.

Question 1: Redressement. (2 points)

1. Proposer une méthode semi-manuelle, nécessitant au plus quatre clics, pour redresser la page (texte horizontal).

2. Comment peut-on automatiser ce procédé?

Indication

On peut demander à l’utilisateur de cliquer sur les quatre coins de la page, puis estimer l’homographie permettant de passer à un rectangle ayant les mêmes proportions.

On peut automatiser procédé de deux façons:

• transformée de Hough pour estimer la position des bords de la page

• détecteur de coins pour estimer la position des coins de la page

Question 2: Élimination du fond. (2 points)

Proposer une méthode permettant de séparer le texte écrit du fond de la page.

Indication

L’approche la plus simple ici consiste à réaliser une binarisation à l’aide d’une méthode de seuillage. Comme il s’agit de texte pas parfaitement uniforme, une méthode adaptative (seuillage local) comme celle de Sauvola donnera un meilleur résultat que le seuillage d’Otsu.

Question 3: Détection du symbole. (4 points)

1. On demande à l’utilisateur ou utilisatrice du programme de dessiner un rectangle autour du symbole à détecter (le symbole de référence). Proposer une solution pour trouver automatiquement tous les symboles similaires dans la page.

2. Comment gérer le cas où le symbole peut changer de taille dans la page?

3. Bonus: comment accélérer la recherche pour ne pas avoir à parcourir toute la page pour chercher le symbole?

Indication

L’approche la plus simple consiste à traiter ce problème de détection comme du template matching. Les symboles sont à peu près tous écrits de la même façon, on peut donc calculer une corrélation croisée entre la boîte du symbole et toutes les régions de l’image. On ne conserve que les pics de corrélation (maxima locaux supérieurs à un seuil).

Si le symbole peut changer de taille, une solution naturelle est d’appliquer le même algorithme que précédemment mais sur une pyramide d’images à différentes échelles (image initiale, image réduite de 3:4, image réduite de 1:2, puis 1:4 etc.). On pourrait aussi faire ce même travail mais avec des descripteurs qui sont invariants à l’échelle, comme les histogrammes de couleur ou les HoG.

Pour le cas bonus, l’optimisation consiste à ne pas effectuer la fenêtre glissante sur toute la page. Dans un premier temps, on peut se contenter de parcourir uniquement les régions qui contiennent du texte (selon notre binarisation de l’étape précédente).

Une optimisation plus poussée (mais moins évidente) consiste à réduire la taille de l’image et du template (par exemple d’un facteur 2). On effectue une première recherche qui sera moins précise (elle aura des faux positifs car, à plus faible résolution, il y aura plus de symboles qui ressemblent au template). Ensuite, on calcule la corrélation croisée complète à résolution initiale seulement sur les zones qui ont bien corrélé à résolution plus basse. En choisissant bien le facteur de réduction, le nombre total d’opérations peut être beaucoup plus faible qu’en effectuant le template matching sur toute l’image de départ.

Fin des questions.